In physics, chaos is something unpredictable. A butterfly flapping its wings somewhere in Guatemala might seem insignificant, but those flits and flutters might be the ultimate cause of a hurricane over the Indian Ocean. The butterfly effect captures what it means for something to behave chaotically: Two very similar starting points—a butterfly that either flaps its wings or doesn’t—could lead to two drastically different results, like a hurricane or calm winds.
But there's also a tamer, more subtle form of chaos in which similar starting points don’t cause drastically different results—at least not right away. This tamer chaos, known as ergodicity, is what allows a coffee cup to slowly cool down to room temperature or a piece of steak to heat up on a frying pan. It forms the basis of the field of statistical mechanics, which describes large collections of particles and how they exchange energy to arrive at a shared temperature. Chaos almost always grows out of ergodicity, forming its most eccentric variant.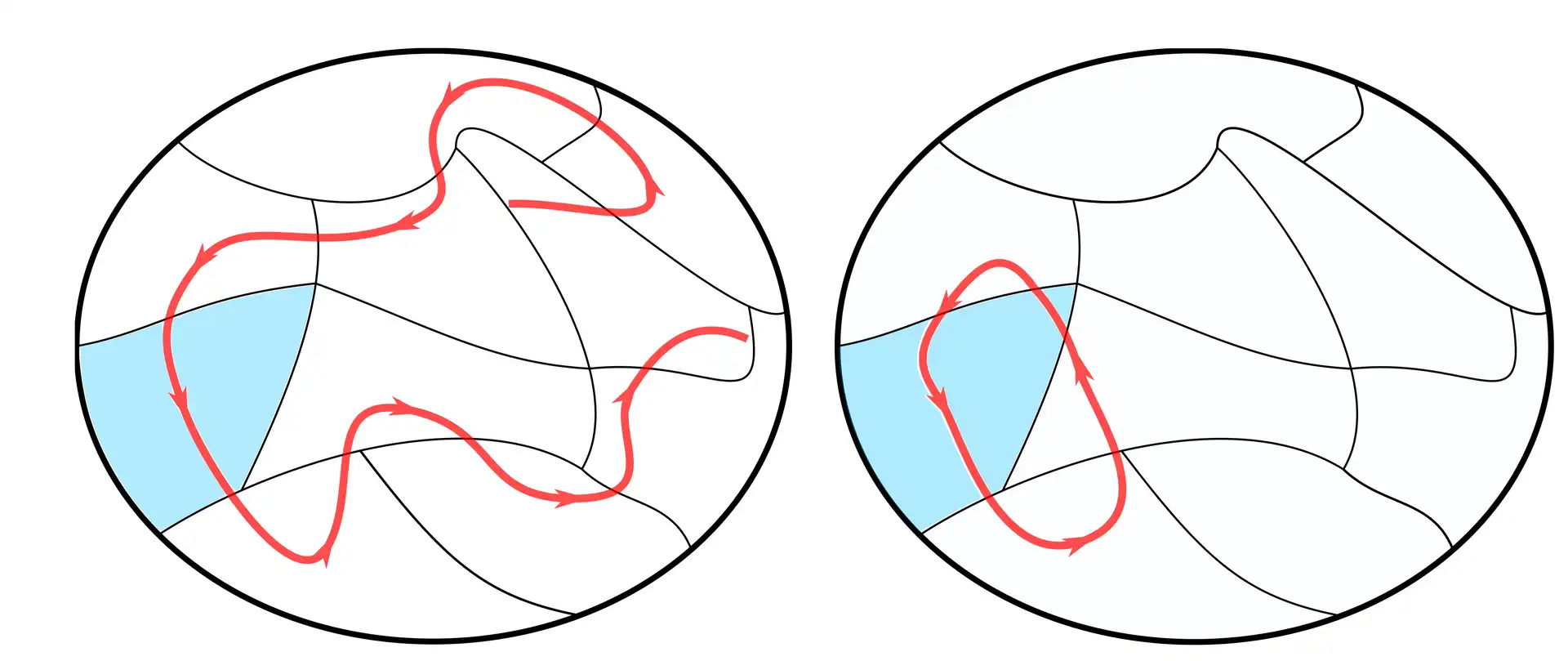 A system is ergodic if a particle traveling through it will eventually visit every possible point. In quantum mechanics, you never know exactly what point a particle is at, making ergodicity hard to track. In this schematic, the available space is divided into quantum-friendly cells, and an ergodic particle (left) winds through each of the cells, while a non-ergodic one (right) only visits a few. (Credit: Amit Vikram/JQI)
A system is ergodic if a particle traveling through it will eventually visit every possible point. In quantum mechanics, you never know exactly what point a particle is at, making ergodicity hard to track. In this schematic, the available space is divided into quantum-friendly cells, and an ergodic particle (left) winds through each of the cells, while a non-ergodic one (right) only visits a few. (Credit: Amit Vikram/JQI)
Where classical, 19th-century physics is concerned, ergodicity is pretty well understood. But we know that the world is fundamentally quantum at the smallest scales, and the quantum origins of ergodicity have remained murky to this day—the uncertainty inherent in the quantum world makes classical notions of ergodicity fail. Now, Victor Galitski and colleagues in the Joint Quantum Institute (JQI) have found a way to translate the concept of ergodicity into the quantum realm. They recently published their results in the journal Physical Review Research. This work was supported by the DOE Office of Science (Office of Basic Energy Sciences).
“Statistical mechanics is based on the assumption that systems are ergodic,” Galitski says. “It’s an assumption, a conjecture, and nobody knows why. And our work sheds light on this conjecture.”
In the classical world, ergodicity is all about trajectories. Imagine an air hockey puck bouncing around a table. If you set it in motion, it will start bouncing off the walls, changing direction with each collision. If you wait long enough, that puck will eventually visit every point on the table's surface. This is what it means to be ergodic—to visit every nook and cranny available, given enough time. If you paint the puck’s path as you go, you will eventually color in the whole table. If lots of pucks are unleashed onto the table, they will bump into each other and eventually spread out evenly over the table.
To translate this idea of ergodicity into the quantum world of individual particles is tough. For one, the very notion of a trajectory doesn't quite make sense. The uncertainty principle dictates that you cannot know the precise position and momentum of a particle at the same time, so the exact path it follows ends up being a little bit fuzzy, making the normal definitions of chaos and ergodicity challenging to apply.
Physicists have thought up several alternate ways to look for ergodicity or chaos in quantum mechanics. One is to study the particle’s quantum energy levels, especially how they space out and bunch up. If the way they bunch up has a particular kind of randomness, the theory goes, this is a type of quantum chaos. This might be a nice theoretical tool, but it’s difficult to connect to the actual motion of a quantum particle. Without such a connection to dynamics, the authors say there’s no fundamental reason to use this energy level signature as the ultimate definition of quantum chaos. “We don't really know what quantum chaos [or ergodicity] is in the first place,” says Amit Vikram, a graduate student in physics at JQI and lead author of the paper. “Chaos is a classical notion. And so what people really have are different diagnostics, essentially different things that they intuitively associate with chaos.”
Galitski and Vikram have found a way to define quantum ergodicity that closely mimics the classical definition. Just as an air hockey puck traverses the surface of the table, quantum particles traverse a space of quantum states—a surface like the air hockey table that lives in a more abstract world. But to capture the uncertainty inherent to the quantum world, the researchers break the space up into small cells rather than treating it as individual points. It's as if they divided the abstract air hockey table into cleverly chosen chunks and then checked to see if the uncertainty-widened particle has a decent probability of visiting each of the chunks.
“Quantum mechanically you have this uncertainty principle that says that your resolution in trajectories is a little bit fuzzy. These cells kind of capture that fuzziness,” Vikram says. “It's not the most intuitive thing to expect that some classical notion would just carry over to quantum mechanics. But here it does, which is rather strange, actually.”
Picking the correct cells to partition the space into is no easy task—a random guess will almost always fail. Even if there is only one special choice of cells where the particle visits each one, the system is quantum ergodic according to the new definition. The team found that the key to finding that magic cell choice, or ruling that no such choice exists, lies in the particle’s quantum energy levels, the basis of previous definitions of quantum chaos. This connection enabled them to calculate that special cell choice for particular cases, as well as connect to and expand the previous definition.
One advantage of this approach is that it's closer to something an experimentalist can see in the dynamics—it connects to the actual motion of the particle. This not only sheds light on quantum ergodicity, quantum chaos and the possible origins of thermalization, but it may also prove important for understanding why some quantum computing algorithms work while others do not.
As Galitski puts it, every quantum algorithm is just a quantum system trying to fight thermalization. The algorithm will only work if the thermalization is avoided, which would only happen if the particles are not ergodic. “This work not only relates to many body systems, such as materials and quantum devices, but that also relates to this effort on quantum algorithms and quantum computing,” Galitski says.
Original story by Dina Genkina: https://jqi.umd.edu/news/embracing-uncertainty-helps-bring-order-quantum-chaos