Unlike speed limits on the highway, most speed limits in physics cannot be disobeyed. For example, no matter how little you care about getting a ticket, you can never go faster than the speed of light. Similarly stringent limits exist for information, too. The speed of light is still the ultimate speed limit, but depending on how information is stored and transmitted, there can be slower limits in practice.
The story gets particularly subtle when the information is quantum. Quantum information is represented by qubits (the quantum version of ordinary bits), which can be stored in photons, atoms or any number of other systems governed by the rules of quantum physics. Figuring out how fast information can move from one qubit to another is not only interesting from a fundamental point of view; it’s also important for more practical purposes, like improving the designs of quantum computers and learning what their limitations might be.
Now, a group of UMD researchers led by Adjunct Associate Professor Alexey Gorshkov—who is a Fellow of the Joint Quantum Institute and the Joint Center for Quantum Information and Computer Science and a physicist at the National Institute of Standards and Technology(link is external)—in collaboration with teams at the University of Colorado Boulder, Caltech, and the Colorado School of Mines, have found something surprising: the speed limit for quantum information can depend on the task at hand. They detail their results in a paper published July 13, 2020 in the journal (link is external)Physical Review X(link is external) and featured in Physics(link is external).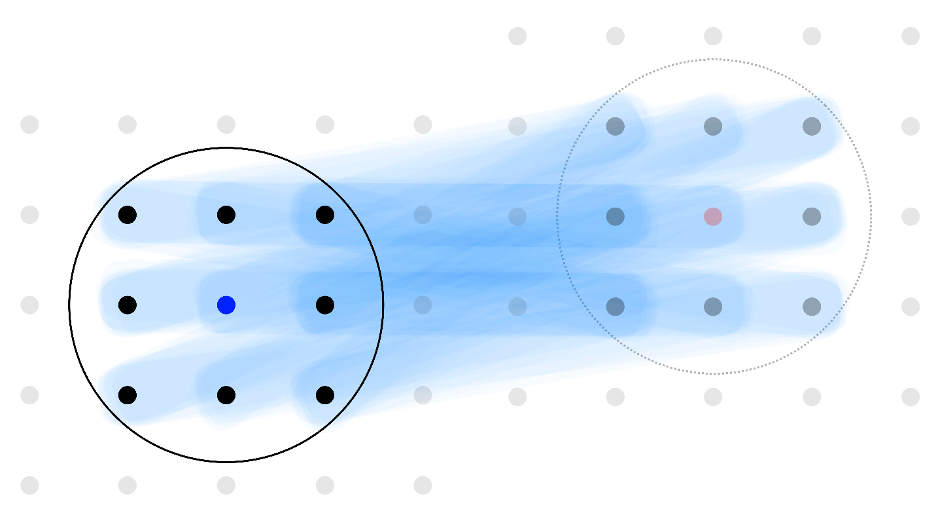
A new protocol for cutting and pasting quantum information first spreads the content of one quantum bit (blue dot) over a region (black circle). Then, it takes advantage of long-range interactions (blue streaks) to transfer the information. Finally, it collects the information at the target quantum bit (red dot). (Credit: Chi-Fang Chen/Caltech)
Just as knowing the speed of light doesn’t automatically let us build rockets that can travel that fast, knowledge of the speed at which quantum information can travel doesn’t tell us how it can be done. But figuring out what sets these speed limits did allow the team to come up with new information transfer methods that approach the theoretical speed limit closer than ever before.
“Figuring out the fastest way to move quantum information around will help us maximize the performance of future quantum computers,” says Minh Tran, a graduate student in physics at UMD and the lead author of the paper.
One procedure subject to these new limits is like a quantum cut and paste: moving the information stored in one qubit to a different one far away. It’s a crucial task that can become a bottleneck as quantum computers get larger and larger. In quantum computers based on superconductors, like Google’s Sycamore(link is external), qubits only really talk to their next-door neighbors. Or, in physics-speak, their interactions are short-range. That means that once you cut a qubit, you’d have to go door to door, cutting and pasting it until you reach the target. The speed limit for this situation was found back in the 1970’s. It’s strict and consistent—it doesn’t ease up no matter how far the information travels.
Things get more complicated—and more realistic for a lot of quantum computing platforms—when you start to consider long-range interactions: qubits that talk not only to the ones directly next to them, but also to neighbors several doors down. Quantum computers built with trapped ions, polar molecules, and Rydberg atoms all have these long-range interactions.
Previous work has shown that in long-range interacting setups, there isn’t always a strict speed limit. Sometimes, the information can travel faster once it’s gone further away from its starting point, and other times its speed isn’t limited at all (except for the ultimate limit set by the speed of light). This depends on the dimensions of the quantum computer (if it’s a chain, a pancake, or a cube) as well as the strength of the long-range interaction (how loudly one qubit can talk to another many doors down).
Finding regimes where these long-range interactions relax the information speed limits carries the promise of making quantum processing much faster. Gorshkov, Tran and their collaborators looked more closely at the regime where the speed limit is not strict—where information is allowed to travel faster as it gets further away from its origin. What they found was surprising: for some applications, the speed limit was indeed loose as previously discovered. But for others, the speed limit was just as strict as in the nearest neighbor case.
This implies that for the same quantum computer the speed limits are different for different tasks. And even for the same task, such as quantum cut-and-paste, different rules can apply in different situations. If you cut-and-paste in the beginning of a computation, the speed limit is loose, and you can do it very quickly. But if you have to do it mid-computation, when the states of the qubits along the way aren’t known, a stricter speed limit applies.
“The existence of different speed limits is cool fundamentally because it shows a separation between tasks that seemed very similar,” says Abhinav Deshpande, a graduate student in physics at UMD and one of the authors of the new paper.
So far, few experimental realizations of quantum computers have been able to take advantage of long-range interactions. Nevertheless, the state of the art is improving rapidly, and these theoretical findings may soon play a crucial role in designing quantum computing architectures and choosing protocols that optimize their efficiency. “Once you get systems that are larger and more coherent,” says Gorshkov, “down the road, these insights will be even more applicable.”
Original story by Dina Genkina
In addition to Tran, Deshpande and Gorshkov, authors on this paper included Chi-Fang Chen, a graduate student in physics at the California Institute of Technology; Adam Ehrenberg, a graduate student in physics at UMD; Andrew Guo, a graduate student in physics at UMD; Yifan Hong, a graduate student in physics at the University of Colorado Boulder; Zhexuan Gong, a former research scientist at JQI who is currently an assistant professor of physics at the Colorado School of Mines; and Andrew Lucas, an assistant professor of physics at the University of Colorado Boulder.