When you brush your hair in the morning, there’s a pretty good chance you’re not thinking about quantum physics. But the way your hair swirls as you brush is actually related to some features of the quantum world.

Important properties of quantum particles are described by topology—a field of mathematics that classifies objects according to how many holes they have. For instance, a coconut is topologically the same as a pizza (no holes), but different from a donut (one hole). Importantly, topology also dictates the kinds of hairdos you can style on these shapes. On a fuzzy coconut, no matter how much you brush, you’ll end up with at least one whorl—a spot that all the nearby hairs swirl around. On the other hand, a hairy donut can be brushed down flat without incurring any unsightly tufts or whorls. It can also have pairs of whorls, swirling in opposite directions, but never a single whorl.

This is not merely a question of fashion. In physical materials, topology can determine many interesting properties, like whether a material conducts electricity or not—particularly at its edges. Additionally, these edge properties are extremely precise and stable—so stable that they now serve as the standard for measuring electrical resistance.

Physicists don’t usually re-shape the materials they study into donuts or attach hairs to them. Instead, they often look at the topology of the quantum states of a particle moving around in the material. The coconut or donut shapes are found in abstract landscapes, inhabited by the possible speeds and directions the particle is moving—in technical language, each point in this space corresponds to a particular momentum. At each momentum, a “hair” sticks out, representing the internal quantum state of the particle. For solid materials, whose atoms line up into repeating crystal structures, the landscape is usually donut-shaped, and quantum whorls either don’t form at all or appear in pairs.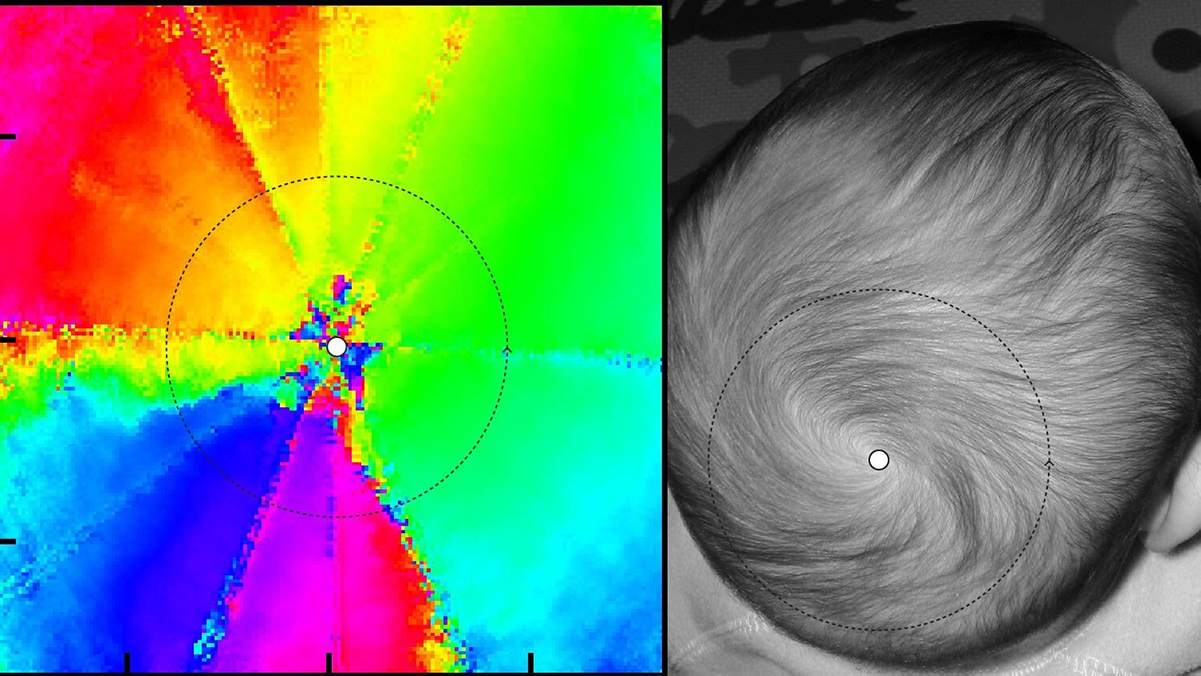Scientist created a swirl around a central point (white dot) in the quantum state of atoms (left), akin to a whorl of hair on a baby’s head (right). (Credit: Ana Valdes/JQI)

Now, a team of JQI researchers has engineered a new kind of topological matter—one with a single whorl—by breaking free from the constraints of crystalline solids. They managed to do this by grooming their atomic states into a whorl situated in an abstract, infinite plane, rather than a coconut or donut shape. The team was led by former UMD graduate student Ana Valdes-Curiel (currently a postdoc at the University of California, Los Angeles) in the group of Adjunct Professor and JQI Fellow Ian Spielman, a fellow at the National Institute of Standards and Technology. They reported their findings in a recent paper published in Nature Communications.(link is external)

In most solids, be they metals, insulators or superconductors, atoms arrange themselves in a repeating grid. Some electrons in the atoms can travel around in this grid, moving up and down or left and right. But no matter where an electron travels, it will end up experiencing deja vu: The grid of atoms repeats, so any given spot in the crystal looks exactly like many others.

This repeating structure has an effect on an electron’s momentum, too. In fact, topologically speaking, it’s as if the electron’s momentum is constrained to the surface of a donut. And since the donut can be brushed smooth, most materials have quantum state “hairs” that are swirl free. (They can also form two whorls, with hairs spiraling around them in opposite directions.)

To create their quantum whorl without the benefit of a neatly arranged crystal, the JQI team took a cloud of rubidium atoms and cooled it down to extremely low temperatures—so cold that quantum effects take over. At these temperatures, the atoms can inhabit only a few distinct quantum states. But, crucially, without the regular order of a crystal, there was no restriction on their momenta—they could move at any speed, up and down as well as left and right, forming a topological landscape of possible momenta akin to an infinite sheet.

Once the atoms were cooled, the team used three laser beams with precisely chosen colors and orientations to shuffle the atoms between three of the possible quantum states in sequence: first to second to third and back to first again. With each hop between states, the lasers imparted a small kick to the atoms, causing atoms in different states to move with slightly different speeds (and thus different momenta). This ensured that the quantum “hairs” pointed in different directions at different momenta and created a swirl around a point in the momentum landscape—the quantum whorl.

“And it turns out with this kind of atom, implementing that idea in a robust way is just super hard,” Spielman says.

Not all states can be manipulated to hop in a circle, and the ones that can are pretty unstable, quickly decaying and heating the cold atomic cloud. They are also easily disturbed by the tiniest changes in the lab’s magnetic field—something as small as a person walking by with a metal keychain can throw the whole thing off.

To mitigate these issues, the researchers employed a technique that they recently pioneered(link is external). They bathed the atoms in a strong, carefully chosen radio-frequency signal before the lasers were turned on. In this field, three stable states are transformed into quantum superpositions of each other, with parts of the other states mixed in. It’s normally impossible to make an atom hop in a circle through these stable states, but once they are jumbled together this restriction is lifted. On top of that, the strong magnetic field of the radio waves inoculated the atoms against small magnetic field disturbances.

They confirmed the novel topology of their cloud of atoms by directly measuring the quantum states they created, at a host of different atom momenta. Traversing their momentum landscape in a loop, they measured what mixture of the constituent states (the first, second, and third states in the circle) the atoms lived in, analogous to looking which direction the hairs were pointing. They confirmed that there was a single swirl at the loop’s center.

One of the most important features of topological materials is the edge effects that occur at an interface with a material that has a different topology. For example, if an insulator happens to have two swirls on its momentum donut, there will be a sharp change whenever it’s bordered by swirl-free air or a vacuum. At the place where materials with different swirl counts meet, something discontinuous has to happen. In this case, the boundary becomes a conductor sandwiched between two insulators. The number of these conducting edge channels exactly corresponds to the topology in the bulk, and they cannot be easily disrupted or destroyed. The discovery and topological explanation of these edge effects was the subject of the 2016 Nobel Prize in Physics(link is external), and has inspired much recent research and development of new types of devices.

“The whole big thing about topology is you get these edge states that are very robust,” says Valdes-Curiel “And now you have this system that is topological, but it doesn’t have the usual topological features. So what happens with the usual bulk-edge correspondence? What kind of edge states do you have? And what kind of topological devices can you build?”

Story by Dina Genkina

In addition to Valdes-Curiel and Spielman, co-authors of this paper included Dimitios Trypogeorgos, a former JQI postdoc now at the at the Institute of Nanotechnology in Lecce, Italy; Qiyu Liang, a postdoc at the JQI; and Russel Anderson, a former visiting researcher at the JQI now at La Trobe University and Q-CTRL.