Physicists love to do scattering experiments.  When they are trying to figure out a new force of nature, or discover a new particle, they fire up the accelerator and shoot tiny particles at their target, and measure what comes out.  Usually they carefully measure the energy and momentum of the incident and exiting particles, and try to learn about what took place in the target from that.  All of this information is summarized in an elegant quantity known as the Scattering Matrix. 

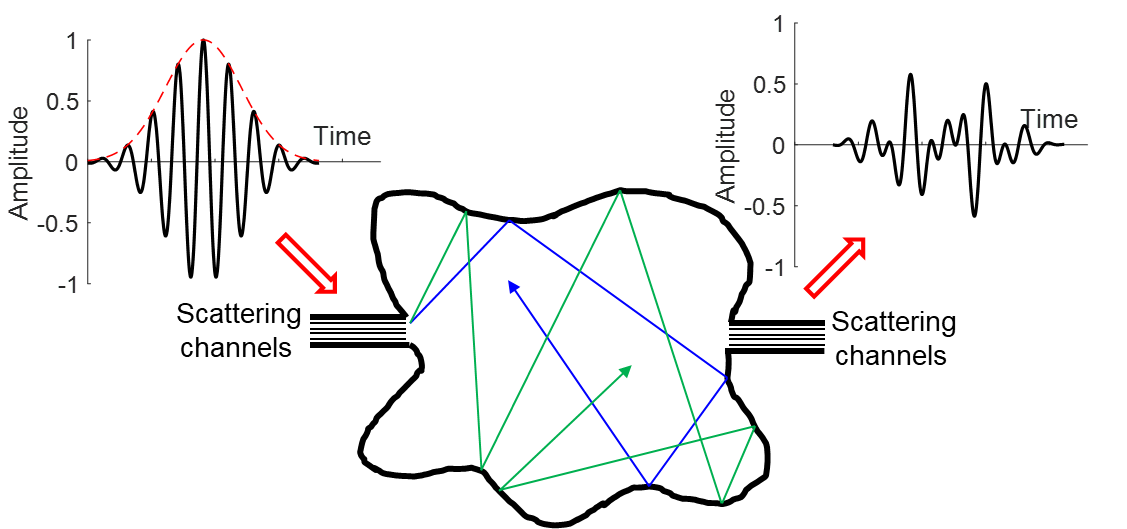Schematic of time delay for scattering of a wave packet from a real-life ray-chaotic billiard. The symmetric and smooth wave packet goes in to the scattering region through one scattering channel and emerges later from another channel as a delayed and strongly distorted pulse. The complex time delay accounts for these changes.

Less studied is the question of how long the particle lingers in the interaction region before coming out.  This quantity is called time delay, and it has been studied since the early days of nuclear physics.  However, time delay never graduated from the confines of its original home, namely relatively simple quantum mechanical settings where the corrupting influences of “dissipation,” “de-coherence” and “dephasing” do not come into play.  Because of the rather restrictive conditions under which time delay was originally defined, it has always been taken to be a real, and generally positive, number.  In a paper published on May 18, 2021 in Physical Review E, Lei Chen, Steve Anlage,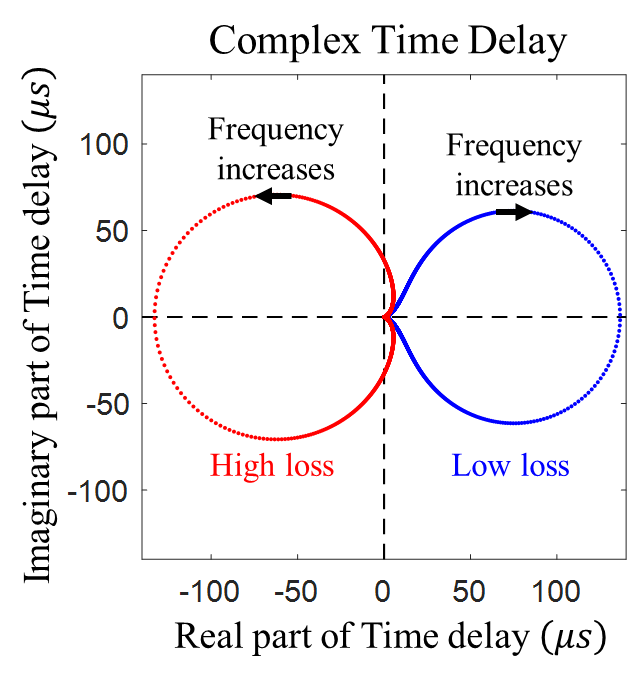Illustration of complex time delay associated with a single resonant mode of a complex scattering system known as a quantum graph. Shown is the evolution of the complex time delay as a function of frequency near the resonance, illustrating how the real and imaginary parts of the time delay form a closed figure in the complex time-delay plane. The cases of two resonances, one with small loss and another with large loss, are shown for illustration. These results are from a simulation of the quantum graph. and Yan V. Fyodorov describe having generalized this time delay to real-world situations where there is dissipation and de-phasing, and created a very useful complex version of time delay.  This generalized time delay has a real part that can be positive or negative, and an imaginary part, which can also have either sign. 

The real part still tells something about the lingering time of the particle, but the imaginary part conveys how much the waves that describe the particle quantum mechanically are distorted by the lossy and disruptive scattering system.  This new quantity gives tremendous insights into the microscopic physics of the scattering system by cleverly encoding information about locations of the poles (infinities) and zeros of the scattering matrix.  Knowing all of those locations is equivalent to knowing essentially everything there is to know about the scattering process.  The exciting thing is that now complex time delay can be used to uncover fundamental properties of scattering systems that arise not just in quantum physics, but also in electromagnetic and acoustic reverberant systems, and the world of the small, but not too small, called mesoscopic physics.

More recently, in a paper published on November 12, 2021 in Physical Review Letters, the same authors have applied their generalized time delay concept to complex scattering systems with many overlapping resonances and zeros.  By looking at the statistical properties of the time delays, they utilized concepts from random matrix theory to reveal information about the distribution of poles in the complex frequency plane.  This deepens the understanding of a broad variety of complicated wave scattering systems, and provides a quantitative tool to characterize and classify them.

To read more, see the paper  "Generalization of Wigner time delay to subunitary scattering systems", in the 1 May 2021 issue of Physical Review E (Vol. 103, No. 5): https://link.aps.org/doi/10.1103/PhysRevE.103.L050203
DOI: 10.1103/PhysRevE.103.L050203

And the follow-up paper “Statistics of Complex Wigner Time Delays as a counter of S-matrix poles: Theory and Experiment,” in the 12 November 2021 issue of Physical Review Letters (Vol. 127, No. 20): https://doi.org/10.1103/PhysRevLett.127.204101
DOI: 10.1103/PhysRevLett.127.204101