The world is a cluttered, noisy place, and the ability to effectively focus is a valuable skill. For example, at a bustling party, the clatter of cutlery, the conversations, the music, the scratching of your shirt tag and almost everything else must fade into the background for you to focus on finding familiar faces or giving the person next to you your undivided attention.
Similarly, nature and experiments are full of distractions and negligible interactions, so scientists need to deliberately focus their attention on sources of useful information. For instance, the temperature of the crowded party is the result of the energy carried by every molecule in the air, the air currents, the molecules in the air picking up heat as they bounce off the guests and numerous other interactions. But if you just want to measure how warm the room is, you are better off using a thermometer that will give you the average temperature of nearby particles rather than trying to detect and track everything happening from the atomic level on up. A few well-chosen features—like temperature and pressure—are often the key to making sense of a complex phenomenon.
It is especially valuable for researchers to focus their attention when working on quantum physics. Scientists have shown that quantum mechanics accurately describes small particles and their interactions, but the details often become overwhelming when researchers consider many interacting quantum particles. Applying the rules of quantum physics to just a few dozen particles is often more than any physicist—even using a supercomputer—can keep track of. So, in quantum research, scientists frequently need to identify essential features and determine how to use them to extract practical insights without being buried in an avalanche of details.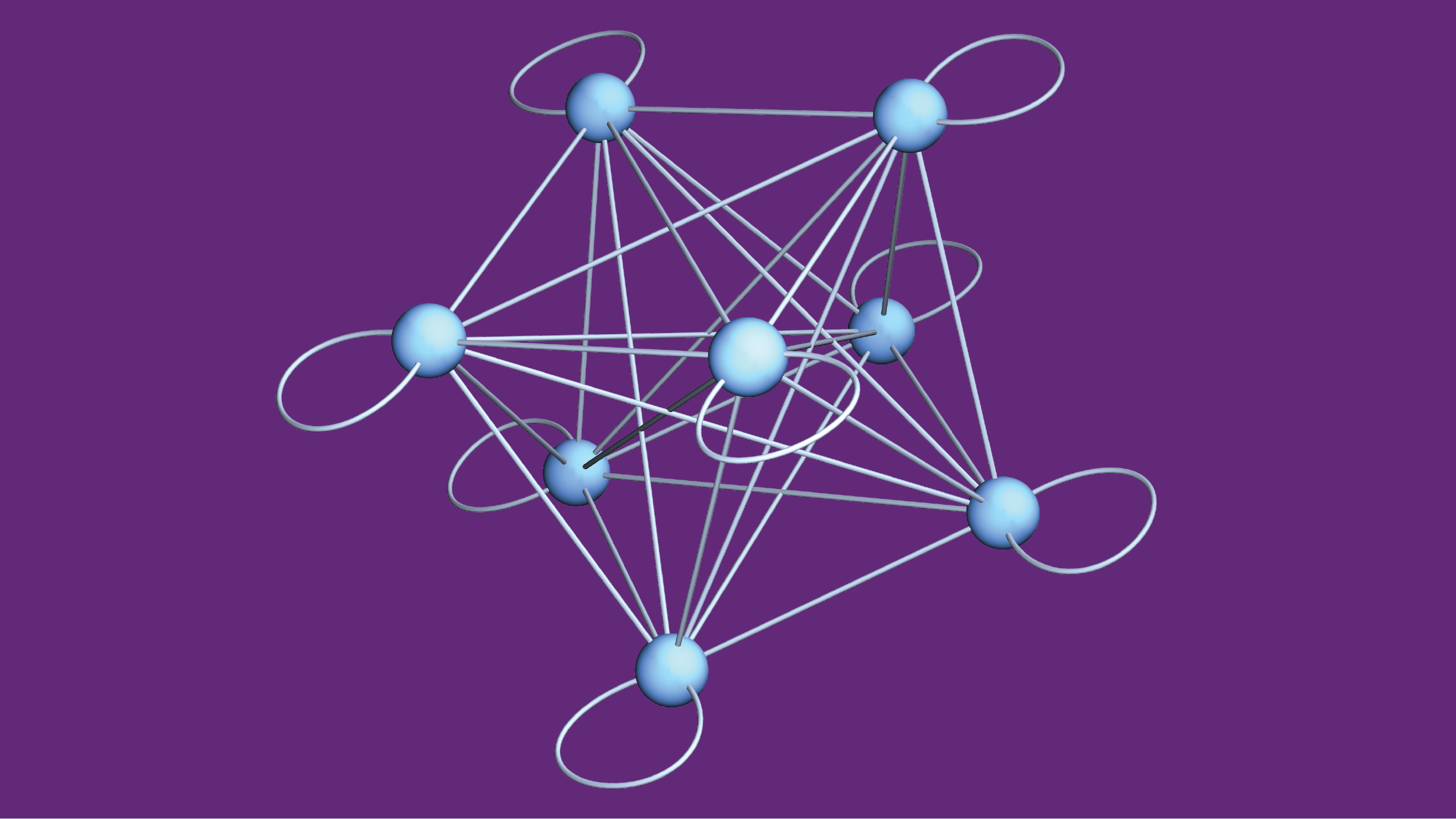
A collection of quantum particles can store information in various collective quantum states. The above model represents the states as blue nodes and illustrates how interactions can scramble the organized information of initial states into a messy combination by mixing the options along the illustrated links. (Credit: Amit Vikram, UMD)
In a paper published in the journal Physical Review Letters in January 2024, Professor Victor Galitski and JQI graduate student Amit Vikram identified a new way that researchers can obtain useful insights into the way information associated with a configuration of particles gets dispersed and effectively lost over time. Their technique focuses on a single feature that describes how various amounts of energy can be held by different configurations a quantum system. The approach provides insight into how a collection of quantum particles can evolve without the researchers having to grapple with the intricacies of the interactions that make the system change over time.
This result grew out of a previous project where the pair proposed a definition of chaos for the quantum world. In that project, the pair worked with an equation describing the energy-time uncertainty relationship—the less popular cousin of the Heisenberg uncertainty principle for position and momentum. The Heisenberg uncertainty principle means there’s always a tradeoff between how accurately you can simultaneously know a quantum particle’s position and momentum. The tradeoff described by the energy-time uncertainty relationship is not as neatly defined as its cousin, so researchers must tailor its application to different contexts and be careful how they interpret it. But in general, the relationship means that knowing the energy of a quantum state more precisely increases how long it tends to take the state to shift to a new state.
When Galitski and Vikram were contemplating the energy-time uncertainty relationship they realized it naturally lent itself to studying changes in quantum systems—even those with many particles—without getting bogged down in too many details. Using the relationship, the pair developed an approach that uses just a single feature of a system to calculate how quickly the information contained in an initial collection of quantum particles can mix and diffuse.
The feature they built their method around is called the spectral form factor. It describes the energies that quantum physics allows a system to hold and how common they are—like a map that shows which energies are common and which are rare for a particular quantum system.
The contours of the map are the result of a defining feature of quantum physics—the fact that quantum particles can only be found in certain states with distinct—quantized—energies. And when quantum particles interact, the energy of the whole combination is also limited to certain discrete options. For most quantum systems, some of the allowed energies are only possible for a single combination of the particles, while other energies can result from many different combinations. The availability of the various energy configurations in a system profoundly shapes the resulting physics, making the spectral form factor a valuable tool for researchers.
Galitski and Vikram tailored a formulation of the energy time uncertainty relationship around the spectral form factor to develop their method. The approach naturally applies to the spread of information since information and energy are closely related in quantum physics.
While studying this diffusion, Galitski and Vikram focused their attention on an open question in physics called the fast-scrambling conjecture, which aims to pin down how long it takes for the organization of an initial collection of particles to be scrambled—to have its information mixed and spread out among all interacting particles until it becomes effectively unrecoverable. The conjecture is not concerned just with the fastest scrambling that is possible for a single case, but instead, it is about how the time that the scrambling takes changes based on the size or complexity of the system.
Information loss during quantum scrambling is similar to an ice sculpture melting. Suppose a sculptor spelled out the word “swan” in ice and then absentmindedly left it sitting in a tub of water on a sunny day. Initially, you can read the word at a glance. Later, the “s” has dropped onto its side and the top of the “a” has fallen off, making it look like a “u,” but you can still accurately guess what it once spelled. But, at some point, there’s just a puddle of water. It might still be cold, suggesting there was ice recently, but there’s no practical hope of figuring out if the ice was a lifelike swan sculpture, carved into the word “swan” or just a boring block of ice.
How long the process takes depends on both the ice and the surroundings: Perhaps minutes for a small ice cube in a lake or an entire afternoon for a two-foot-tall centerpiece in a small puddle.
The ice sculpture is like the initial information contained in a portion of the quantum particles, and the surrounding water is all the other quantum particles they can interact with. But, unlike ice, each particle in the quantum world can simultaneously inhabit multiple states, called a quantum superposition, and can become inextricably linked together through quantum entanglement, which makes deducing the original state extra difficult after it has had the chance to change.
For practical reasons, Galitski and Vikram designed their technique so that it applies to situations where researchers never know the exact states of all the interacting quantum particles. Their approach works for a range of cases spanning those where information is stored in a small chunk of all the interacting quantum particles to ones where the information is on a majority of particles—anything from an ice cube in a lake to a sculpture in a puddle. This gives the technique an advantage over previous approaches that only work for information stored on a few of the original particles.
Using the new technique, the pair can get insight into how long it takes a quantum message to effectively melt away for a wide variety of quantum situations. As long as they know the spectral form factor, they don’t need to know anything else.
“It's always nice to be able to formulate statements that assume as little as possible, which means they're as general as possible within your basic assumptions,” says Vikram, who is the first author of the paper. “The neat little bonus right now is that the spectral form factor is a quantity that we can in principle measure.”
The ability of researchers to measure the spectral form factor will allow them to use the technique even when many details of the system are a mystery. If scientists don’t have enough details to mathematically derive the spectral form factor or to tailor a custom description of the particles and their interactions, a measured spectral form factor can still provide valuable insights.
As an example of applying the technique, Galitski and Vikram looked at a quantum model of scrambling called the Sachdev-Ye-Kitaev (SYK) model. Some researchers believe there might be similarities between the SYK model and the way information is scrambled and lost when it falls into a black hole.
Galitski and Vikram’s results revealed that the scrambling time became increasingly long as they looked at larger and larger numbers of particles instead of settling into conditions that scrambled as rapidly as possible.
“Large collections of particles take a really long time to lose information into the rest of the system,” Vikram says. “That is something we can get in a very simple way without knowing anything about the structure of the SYK model, other than its energy spectrum. And it's related to things people have been thinking about simplified models for black holes. But the real inside of a black hole may turn out to be something completely different that no one's imagined.”
Galitski and Vikram are hoping future experiments will confirm their results, and they plan to continue looking for more ways to relate a general quantum feature to the resulting dynamics without relying on many specific details. They and their colleagues are also investigating properties of the spectral form factor that every system should satisfy and are working to identify constraints on scrambling that are universal for all quantum systems.
Original story by Bailey Bedford: https://jqi.umd.edu/news/focused-approach-can-help-untangle-messy-quantum-scrambling-problems
This research was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award No. DE-SC0001911.