- Details
-
Published: Monday, February 26 2024 09:24
In the menagerie of exotic materials, superconductors boast their own vibrant ecosystem.
All superconductors allow electricity to flow without any resistance. It’s their hallmark feature. But in many cases, that’s where the similarities end.
Some superconductors, like aluminum, are conventional—run-of-the-mill, bread-and-butter materials that are well understood and hold no surprises. Others are deemed unconventional: They are not yet fully understood, but that seem to follow a known pattern. But one material—uranium ditelluride (UTe2)—defies classification, continuously baffling scientists with a plethora of unexpected behaviors.
“At first, we thought this was going to be another interesting superconductor like some other uranium compounds that have been studied in the past,” says Johnpierre Paglione, a professor of physics at the University of Maryland (UMD) and the director of the Quantum Materials Center (QMC). “But at this point, it's gone beyond that. And it's become a much richer example of how crazy a superconductor can get.”
Most superconductors start doing their resistance-less thing when they get super cold. But temperature is only one of the knobs available to researchers studying a material in the lab. Some materials slip into superconductivity when you dial in other aspects of their environment, like the pressure they’re subjected to or the strength of a magnetic field they’re bathed in. UTe2 isn’t fussy about these properties, and it happily hosts superconductivity in all kinds of different situations. And as researchers continue studying the material, they are finding more questions than answers.
“This one material seems to do 100 different things,” says Nicholas Butch, who is a physicist at the National Institute of Standards and Technology (NIST) and a member of QMC. “Somebody asked me after one of my talks ‘What right does one material have to do all these things?’ and I said ‘Right?’”
Butch and Paglione, together with colleagues at UMD, NIST, QMC and elsewhere, have been at the forefront of exploring the many wonders of UTe2. Postdocs Shang Ran and Corey Frank, working at both NIST and QMC have spearheaded many of the efforts, from discovering superconductivity in the material to testing samples at National High Magnetic Field Laboratory facilities around the country and experimenting with different preparation techniques. And the buzz around UTe2 is catching on: QMC has been sharing the samples they synthesize with researchers at other universities, including the University of Illinois at Urbana-Champaign and Cornell University, and further study by these groups resulted in the discovery of yet more unexpected behaviors. 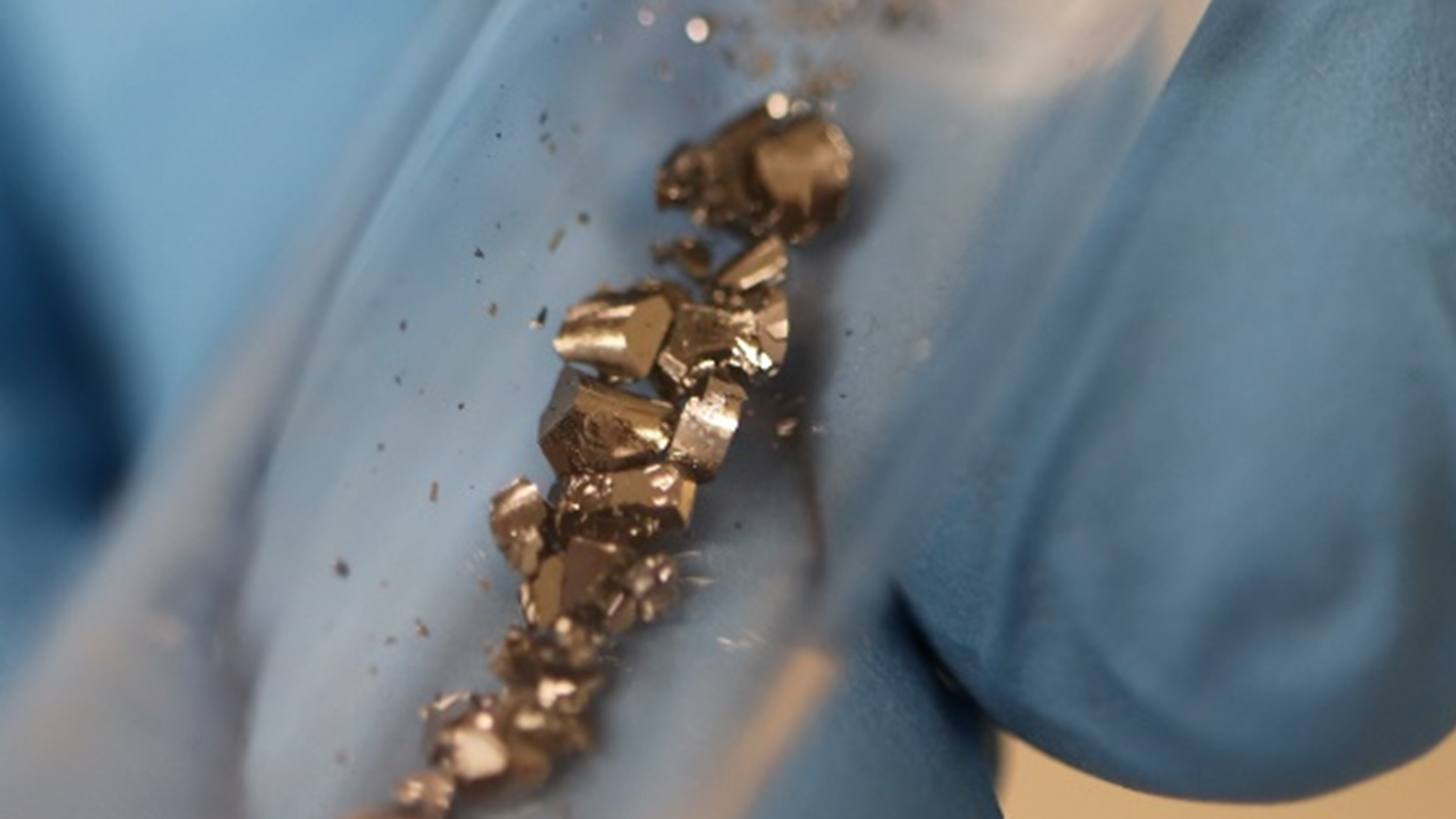 Uranium ditelluride (UTe2)
Uranium ditelluride (UTe2)
A serendipitous discovery
Back in 2018, UMD and NIST postdoc Shang Ran was trying to synthesize U7Te12—a mixture of uranium and tellurium that’s predicted to have intriguing magnetic properties. Instead, Ran kept accidentally making UTe2. He found some literature from the 1960s suggesting UTe2 might have some interesting magnetic properties as well, and after consulting Butch, the two decided to cool it down anyway to see what would happen. Ran stuck the sample into a special helium-powered refrigerator. To his surprise, superconducting currents started to flow.
“We accidentally synthesized this uranium ditelluride, and it turned out it’s a superconductor. So, miracle!” Ran says. “That certainly brought excitement to the community and to our research.”
Ran became captivated with UTe2, and the team went on to poke and prod at it to try to understand its superconducting properties. To start, they set out to explore one of the key behaviors for any superconductor—its response to a magnetic field.
In superconductors, electrons floating around in the material couple up, forming what’s known as Cooper pairs. These pairs act in concert with each other, and with the other pairs around them, allowing the electrons to flow without resistance. However, a strong magnetic field can break up the pairs, destroying the superconducting magic. One of the main signatures of a superconductor is how much magnetic juice it can withstand, and Ran and his collaborators set out to find this landmark for uranium ditelluride.
To their surprise, uranium ditelluride remained a superconductor as they turned the field all the way up to the maximum power they has access to in the lab—20 tesla. That’s the combined magnetic strength of about two thousand fridge magnets, or ten times the magnetic field in an MRI machine. “I was shocked when [graduate student Chris Eckgerg] showed me the data,” says Ran. “I asked him ‘Did you measure correctly?’ We measured again and it was all correct. So, we realized, okay, there's some very strange thing going on.”
It wasn’t until they brought the material to the National High Magnetic Field Laboratory in Tallahassee, Florida that they finally found a magnet strong enough to tear apart UTe2’s Cooper pairs: It took an astounding 35 tesla to break the bond. For comparison, the first superconductor ever discovered—mercury—loses its superconductivity at a mere 0.1 tesla. This tipped off Ran, Butch, and the others that UTe2 was no conventional superconductor. They guessed that the electrons inside UTe2 form Cooper pairs in an unusually resilient way.
A special kind of dance
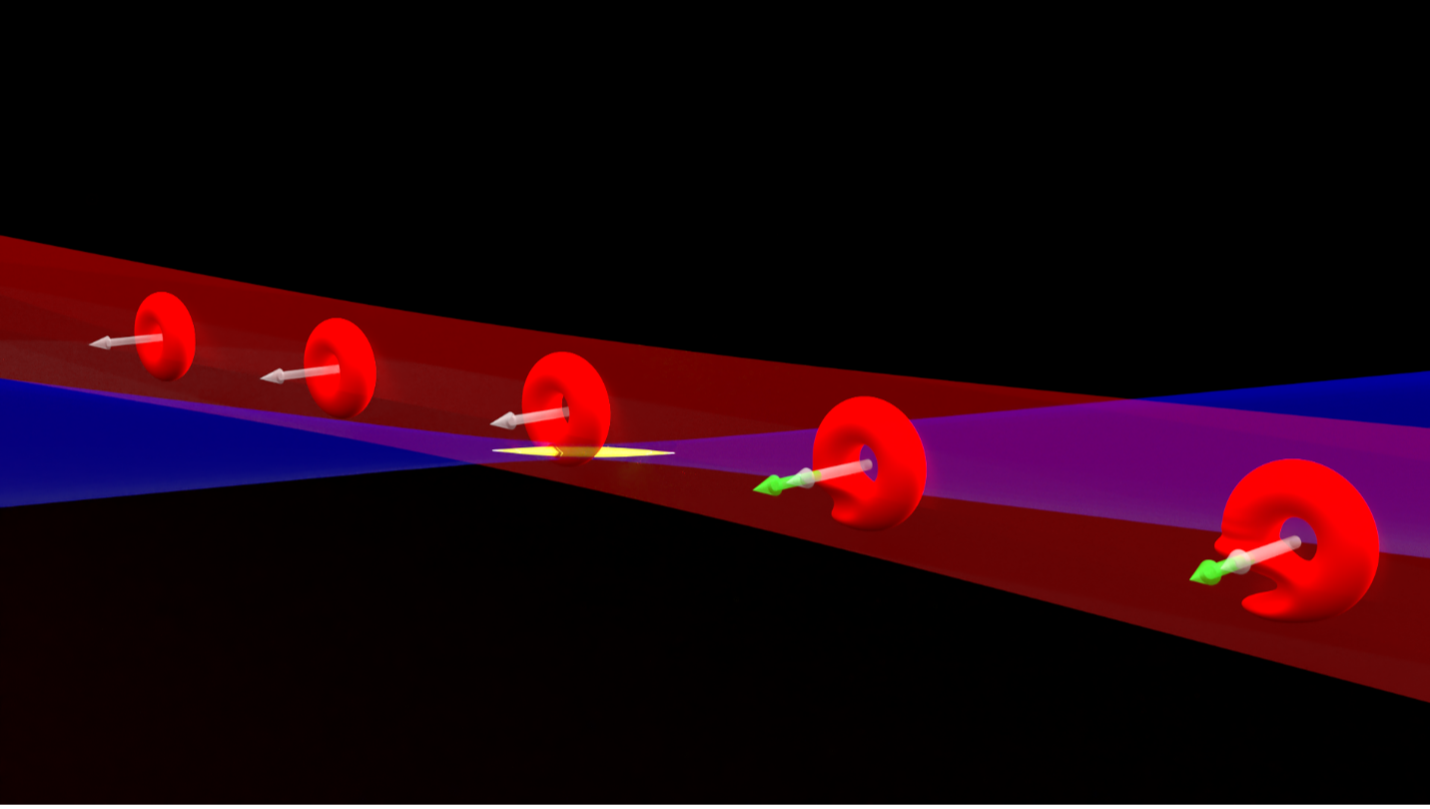
The electrons in a superconductor are kind of like a group of couples on a dance floor. In conventional superconductors, the electron pairs dance together in a straight line, a simple dance where partners mirror each other known as spin-singlet pairing. This synchronized movement allows them to glide effortlessly across the dance floor without any hindrance. However, in some unconventional superconductors, the electron pairs dance in swirly circles, spinning around each other as they glide across the dance floor. This unique dance style, known as spin-triplet pairing, gives them a different kind of coordination.
One consequence of this swirly dance pattern is that breaking up the partners with a magnetic field is much harder, which would explain the high magnetic field UTe2 could withstand. To check if that was going on inside UTe2, the QMC team collaborated with the group of Yuji Furukawa at Iowa State University. The Iowa team used their best techniques for distinguishing between the electron dance patterns, nuclear magnetic resonance spectroscopy. These studies confirmed Ran’s suspicions that UTe2 is a rare spin-triplet superconductor.
Fewer than a dozen materials are suspected of spin-triplet pairing, and the other candidates are difficult to study—they are either hard to synthesize reliably or they only become superconducting under intense pressures or extremely low temperatures. Uranium ditelluride appears to be the most user-friendly spin-triplet superconductor to date, presenting a rare opportunity for researchers.
“This is the only triplet superconductor I know that can be studied by so many different probes,” says Vidya Madhavan, a condensed matter physicist and professor at the University of Illinois at Urbana-Champaign (UIUC) who is a longtime collaborator of the QMC team.
In addition to satisfying a physicist’s basic curiosity, spin-triplet superconductors might be useful as platforms for quantum computing. Spin-triplet pairing is a necessary ingredient for a yet rarer property that hasn’t been confirmed in any superconductor to date—a non-trivial topology. If spin-triplet pairing imbues electron couples with killer dance moves, a non-trivial topology warps the whole dance floor with curves and twists, radically changing the dance patterns of all the couples en masse.
In the months following the discovery of UTe2’s swirly dance patterns, some evidence suggested that UTe2 might not only be a spin-triplet superconductor but also possess that topological special sauce. The evidence is not yet conclusive, but researchers are hard at work trying to sort this out, as well as understand more about what makes UTe2 tick. And their sleuthing keeps turning up more surprises.
Superconductivity raised from the dead (and the never-born)
Ran and his labmates were wondering why 35 tesla seemed to be the magic number that broke superconductivity in UTe2. In search of clues, they went back to the National High Magnetic Field Lab. They kept turning up the magnetic field even higher, looking at how the non-superconducting chunk responded. They also tilted the sample, putting the magnetic field off-kilter from UTe2’s natural crystal structure.
Shockingly, as they kept rotating the sample, superconductivity reappeared at a field of 40 tesla. This was strange. Turning the field up really high killed the superconductivity, but if you kept going it came back to life. This phenomenon was termed Lazarus superconductivity after the biblical figure raised from the dead. Lazarus superconductivity is extremely rare, though not entirely unprecedented. It’s cropped up in a handful of materials before, and scientists think they have plausible mechanisms for explaining the effect. But none of those mechanisms seemed applicable to UTe2.
In 2020, Ran joined the physics department at Washington University in St Louis, passing the torch of Butch’s QMC lab to a new postdoctoral researcher, Corey Frank. Frank had just completed her PhD in solid-state chemistry—the perfect background for mastering different ways of concocting the UTe2 crystal. She played with the initial concentrations of the starting materials as well as precise techniques and temperatures of preparation. Among other things, Frank developed a protocol for making UTe2 samples that are just shy of superconducting by making them intentionally just a bit dirty, peppering the crystals with purposefully introduced defects. These defects gum up the pathways by which electrons pair up and find their dance partners, preventing the development of superconductivity. “You can learn a lot about a phase by studying what kills it,” Frank says.
Frank and her colleagues made a purposefully dirty sample and took it with them on another trip to the National High Magnetic Field Laboratory, this time in Los Alamos, New Mexico. They stuck the sample into the huge magnets and cranked up the field. Once the field was high enough and the sample had the right orientation, the resistance through the material dropped to zero—superconductivity was revived.
“I was so excited,” Frank recalls. “You're not allowed to jump when you're on the platform of a high-field magnet, but I had to get down from the magnet so I could jump. It was amazing.”
This was completely unprecedented. In all the previous Lazarus superconducting materials, the mechanism behind the rebirth was presumed to involve recreating the conditions at a low magnetic field. Here, recreating conditions at a low magnetic field would not result in superconductivity because the samples had intentional defects, and yet there it was—superconductivity raised not from the dead, but from the never-born, a high-field superconducting phase all its own. The team reported this phenomenon last year in a preprint.
“We know how high field superconductivity works, the rules that govern that, and this one breaks those rules,” Frank says. “So the fact that we have this much more robust high-field phase is wild. I cannot overemphasize how unexpected it is.”
The authors have some ideas of what could be causing this behavior, and they say further experiments are needed to figure out if those ideas are correct. For now, the experiments are on hold as they require even stronger magnetic fields than the National High Magnetic Field Laboratory currently offers. In the meantime, the QMC team is still studying how this superconductivity dies, comparing their revived samples to others in search of a pattern.
Making waves
Over many years Ran, Frank, and other members of the Butch lab have mastered the dual feats of growing pure uranium ditelluride crystals and studying their overall behavior—superconductivity, response to magnetic fields, and more. But they lacked the tools and expertise to zoom in on the microscopic, atom-by-atom behavior of UTe2. So they’ve enlisted the help of Vidya Madhavan’s team at UIUC.
In her lab, Madhavan has a scanning tunneling microscope (STM). An STM works by bringing a bit of metal tapered down to a tiny, fine point extremely close to the surface of a sample—so close that electrons from the sample can hop over to the conducting tip, or vice versa. By measuring how many electrons make the jump, scientists can learn a lot about the microscopic structure of a material, including where the electrons are on the surface of the sample.
The Butch group sent Madhavan a sample, and Anuva Aishwarya, a graduate student at UIUC who led the study, placed a sample of UTe2 into the scanning tunneling microscope. The team cooled the material just shy of its superconducting temperature, and they stumbled upon another surprise: The electrons didn’t follow the ups and downs of UTe2’s crystal structure. Instead, they clustered together and then apart, forming waves of charge frozen into the surface with a pattern all their own.
These kinds of charge density waves are uncommon but not unprecedented. However, the measurements performed by Ran, Frank or others at QMC didn’t show any indication that a charge density wave might be found in UTe2. To Madhavan and her team, this came out of nowhere.
To try to understand what they were seeing, Aishwarya and her lab mates probed the behavior of these waves in different temperatures and magnetic fields. They found that, in a magnetic field, the charge density wave seemed intimately related to superconductivity itself. As they turned up the field, the charge density wave broke down at precisely the same field strength as superconductivity. This tipped off Madhavan and her collaborators at UIUC that maybe this wave had some relationship to the superconductivity in uranium ditelluride.
If you want to pick out individual electrons, a regular STM is great. But if you want to peer inside the dance patterns of electron couples in a superconductor, you need an STM armed with a special kind of tip—one that is itself a superconductor. The team of Seamus Davis at Cornell University had just such a superconducting tip. They became intrigued by Madhavan’s results and got in on the action. They obtained another sample from the QMC team and stuck it in their specialized STM. They found that the electron pairs behaved similarly to the lone electrons. Here, too, the pairs clustered together and apart, forming a so-called pair density wave with the same beat as the charge density wave observed by Madhavan. This is the first time such a pair density wave has been found in a spin-triplet superconductor.
As with many aspects of UTe2, the origins of the charge and pair density waves remain far from clear. But, Ran comments, these waves are a fairly common feature in unconventional spin-singlet superconductors. This may provide clues for how all these different strange superconductors are connected. “We eventually need to understand unconventional superconductivity overall,” Ran says. “And having this common theme I think is very important for theorists.”
While theorists are hard at work trying to crack the puzzle of unconventional superconductivity, Ran, Butch, and other researchers are continuing to explore all that UTe2 has in store. “It's really rich. It’s a great place to explore,” says Butch. “This one material underscores how little we know about spin triplet physics. It’s as if we are writing textbooks about it right now. So that's actually very exciting.”
Story by Dina Genkina
 (Credit: Time is Slipping Away (cropped) from Bennilover on Flick under CC BY-ND 2.0 DEED)
(Credit: Time is Slipping Away (cropped) from Bennilover on Flick under CC BY-ND 2.0 DEED)